Neutrons ---- with their wavelengths and energies comparable to atomic spacing and lattice vibrations in solids ---- have played a unique role in determining the static and dynamic lattice and magnetic properties of the TMOs. Some of the reasons for this are as follows: 1) Neutrons are scattered by the nucleus. Light atoms such as hydrogen and oxygen scatter just as strongly as heavier atoms. 2) The neutron carries a magnetic moment that interacts with localized magnetic ions and unpaired itinerant electrons in solids. 3) Neutron is a weak interacting probe. Neutron scattering cross section is determined by the static and dynamic correlation functions of the system, without the need for correcting the influence of the probe. 4) Neutrons are a highly penetrating bulk probe and therefore insensitive to surface imperfections.

Since most Mott insulators such as the parent compounds of high-T_c superconductors and CMR manganites have long range AF order, it is natural to ask what role magnetism has, if any, on the anomalous properties of these materials. Neutron magnetic scattering can determine the energy and momentum dependence of the imaginary part of the dynamical susceptibility or c"(Q,w), information crucial in addressing this question. For copper oxides, since superconducting state is obtained after electron- or hole-doing into the AF state with exchange coupling J, the same coupling could lead to the formation of spin singlets, a prerequisite for superconductivity. While the origin of these two phenomena appear to be related, it is hard to imagine a greater difference in the physical properties between an insulator and a superconductor. The central problem of high-T_c superconductivity is to understand the precise relationship between these two fundamental states of matter and the phase transition between them. Such an understanding would give a unified description of the phase diagram of the high-T_c cuprates and related materials such as organic superconductors and heavy fermion superconductors, and reveal the origin of the pseudogap physics in the underdoped regime. The focus of our program is to use neutron scattering to understand the fundamental properties highly correlated electron materials.

Understanding how MIT occurs echo in TMOs poses one of the most profound intellectual challenges in the physical sciences today. This is because TMOs are often characterized by physical complexity resulting from the coexistence and competition between different kind of order involving charge, orbital, lattice, and spin degrees of freedom. The relationship between these degrees of freedom is often synergistic and non-linear. The complexity of TMOs is directly responsible for their tunability. The balance between competing phases is very subtle and small changes in the composition and/or external condition can produce large changes in the physical properties. For example, while it is well-known that hole-doped (p-type) high-T_c superconductivity arises from doping a Mott insulating phase with static long-range AF order (Fig. 1), superconductivity in electron-doped (n-type) materials can only be realized after annealing the as-grown sample in argon environment to remove excess oxygen. Therefore, a minor change in oxygen concentration can induce MIT and superconductivity in the n-type copper oxides. Although 17 years have passed since their discovery, understanding the microscopic mechanism which is responsible for the amazing properties of these copper oxides is still at the frontier of condensed-matter physics. Similarly, MIT transition can also occur in CMR manganites by either application of a magnetic field or changes lattice disorder.

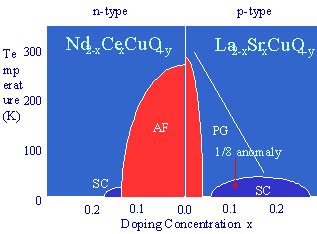
Fig. 1 Phase diagram for single layer electron- and hole-doped copper oxides. The abbreviations are as follows: SC = superconductivity, AF = antiferromagnetic insulator, PG = pseudo-gap phase, anomalous metal.

It is well-known that band filling in noninteracting or weakly interacting electron systems determines its electrical transport properties. An insulator has a completely filled electrons at the highest filled band while a metal has a partially filled band. For these materials, the metal-insulator transition (MIT) occurs through tuning the top-level electron occupation. However, for strongly electron interacting systems such as many transition metal oxides (TMOs) with a partially filled d-band, a large Coulomb repulsion between the outer most d-electrons on the same lattice site would split the highest filled band into two: the lower one (lower Hubbard band) corresponds to single electron occupation while the upper one (upper Hubbard band) to double occupation. With exactly one electron per site (half-filled), the lower Hubbard band is full, and the system forms an insulating state called the Mott insulator. Most Mott insulators have AF long-range order at zero temperature due to Heisenberg coupling between neighboring spins. Once a Mott insulator is doped away from the half-filled case, the system should in principle become metallic. However, strong coupling among spin, charge, and orbital degrees of freedom often makes this regime an anomalous metallic phase which exhibits many unusual physical phenomena such as high-T_c superconductivity, colossal magnetoresistance (CMR) effect and etc